Huffman-Kodierung

Kompression von Text mit Beispielcode in Python

Die Huffman-Codierung bildet die Grundlage für die Kompression (und Dekompression) von Daten. In diesem Beitrag geht es um die entsprechende Datenstruktur (den Huffman-Baum) mit den zugehörigen Algorithmen (Aufbau des Baums, Kompression und Dekompression). Dabei soll es ausschliesslich um Text (und nicht um Binärdaten) gehen, womit sich die ganzen Vorgänge leicht veranschaulichen lassen.

Auftretenshäufigkeit und Komprimierbarkeit

Als Ausgangslage soll der Text „abracadabra“ dienen. Der Buchstabe ‚a‘ kommt darin ganze fünf mal vor, die Buchstaben ‚c‘ und ‚d‘ jedoch je nur einmal. Diesen Umstand macht sich die Huffman-Codierung zu Nutze, indem häufig vorkommende Zeichen mit kurzen Bitsequenzen codiert werden, während die selteneren Zeichen längere Bitsequenzen erfordern.

Zunächst wird die Häufigkeiten der Buchstaben gezählt:

• ‚a‘: 5
• ‚b‘: 2
• ‚r‘: 2
• ‚c‘: 1
• ‚d‘: 1

Aufbau des Huffman-Baums

Als nächstes soll der Kodierungsbaum aufgebaut werden. Dies geschieht „von unten“, d.h. man fängt bei den seltensten Zeichen an. Hierzu muss die Liste aufsteigend nach Häufigkeit und Zeichen sortiert werden:

• ‚c‘: 1
• ‚d‘: 1
• ‚b‘: 2
• ‚r‘: 2
• ‚a‘: 5

Die einzelnen Zeichen mit Häufigkeit bilden die Blätter des Baums:

Nun sollen je zwei Blätter zu einem Ast zusammengefügt werden. Der Ast enthält einerseits eine Liste der darunter kodierten Zeichen, andererseits die Summe der Zeichenhäufigkeit. Die Blätter ‚c‘ und ‚d‘ werden also zu einem Knoten zusammengefasst:

• „cd“: 2
  • ‚c‘: 1
  • ‚d‘: 1
• ‚b‘: 2
• ‚r‘: 2
• ‚a‘: 5

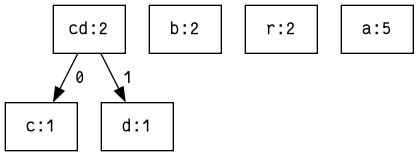
Die Knoten werden erneut nach den gleichen Kriterien sortiert:

• ‚b‘: 2
• „cd“: 2
  • ‚c‘: 1
  • ‚d‘: 1
• ‚r‘: 2
• ‚a‘: 5

Zwar haben ‚b‘ einerseits und ‚c‘/‚d‘ zusammen andererseits die gleiche Häufigkeit, aber es soll auch alphabetisch sortiert werden, damit die Reihenfolge immer wohldefiniert ist. Das Blatt für ‚b‘ und der Knoten für „cd“ werden zu einem neuen Knoten „bcd“ zusammengefügt:

• „bcd“: 4
  • ‚b‘: 2
  • „cd“: 2
    • ‚c‘: 1
    • ‚d‘: 1
• ‚r‘: 2
• ‚a‘: 5

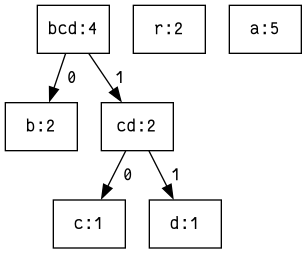
Erneut wird die Liste sortiert:

• ‚r‘: 2
• „bcd“: 4
  • ‚b‘: 2
  • „cd“: 2
    • ‚c‘: 1
    • ‚d‘: 1
• ‚a‘: 5

Und das Spiel kann weitergeführt werden, bis alle Knoten in den Baum integriert worden sind:

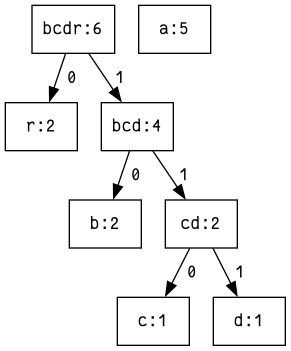
Und schliesslich:

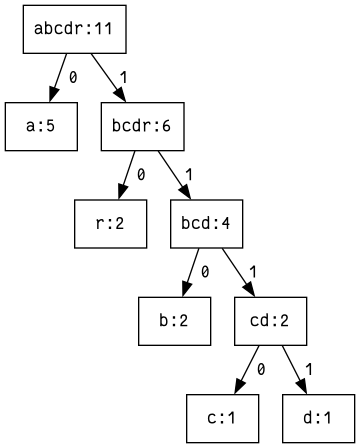
Kompression durch Huffman-Kodierung

Dem geneigten Betrachter dürften die Nullen (an der jeweils linken) und Einsen (an der jeweils rechten Kante) aufgefallen sein. Diese dienen der eigentlichen Kodierung des Textes. Man nehme eine leere Liste [], den ersten Buchstaben des zu kodierenden Textes (‚a‘ von „abracadabra“) und beginne beim obersten Knoten. Da der Baum für diese Zeichenfolge aufgebaut worden ist, müssen alle Buchstaben im Wurzelknoten vorhanden sein. Nun wird das Zeichen ‚a‘ in den beiden Unterknoten gesucht. Da dieses Zeichen im linken Unterknoten zu finden ist, wird die 0 der Liste hinzugefügt: [0].

Gleichermassen wird mit dem Zeichen ‚b‘ verfahren, das mit der Bitfolge [1 1 0] kodiert wird. Die Liste ist nun auf [0 1 1 0] angewachsen. Damit sind zwei Buchstaben mit vier Bits kodiert worden.

Bevor nun die ganze Zeichenfolge „abracadabra“ abgearbeitet wird, was später mit einem Python-Programm erfolgt, soll an dieser Stelle die Dekodierung ausgehend von der Bitfolge [0 1 1 0] versucht werden.

Dekompression durch Huffman-Dekodierung

Der Vorgang beginnt beim Wurzelknoten mit der leeren Zeichenfolge „“. Dem ersten Bit folgend gelangt man zum Knoten ‚a‘, der zugleich ein Blatt ist. So wird der Zeichenkette dieses ‚a‘ hinzugefügt: „a“.

Es bleibt die Bitfolge [1 1 0], mit der wiederum beim Wurzelknoten begonnen werden soll. Es werden nacheinander die Knoten „bcdr“, „bcd“ und schliesslich ‚b‘ besucht. Das ging gut: die Bitfolge war beim Erreichen des Blattes erschöpft, und das ‚b‘ kann der Zeichenkette hinzugefügt werden, die nun „ab“ lautet.

Das Prinzip sollte also verstanden sein. Der ganze Vorgang des Baum-Aufbaus, der Kodierung und Dekodierung wird automatisiert, wozu Python zum Einsatz kommen soll.

Implementierung in Python

Zunächst einmal wird eine Datenstruktur für den Baum benötigt, bzw. für dessen Knoten (Nodes). Neben einer Liste von Zeichen und dem Gewicht werden auch Referenzen auf Unterknoten links und rechts benötigt. So ein Node liesse sich als Klasse oder Dictionary umsetzen; eine namedtuple ist hierfür ein guter Kompromiss:

from collections import namedtuple

Node = namedtuple('Node', 'chars weight left right')

left = False
right = True

Die Variablen left und right sind Aliase für die Bits 0 und 1 (bzw. True und False), die später zum Einsatz kommen werden.

Aufbau des Baumes

Im ersten Schritt können die Blätter (Leaves) als je ein Node pro Buchstabe erstellt werden. Hierzu müssen die Auftretenshäufigkeiten im urpsrünglichen Text gezählt werden:

def count_frequencies(text):
    freqs = {}
    for c in text:
        freqs[c] = freqs.get(c, 0) + 1
    return [Node([c], n, None, None) for c, n in freqs.items()]

In einem Dictionary namens freqs wird die Häufigkeit pro Buchstabe gezählt. mit einer list comprehension wird daraus eine Reihe von Knoten erzeugt; jeweils mit Zeichen und Anzahl; jedoch noch ohne Referenzen links und rechts.

Im nächsten Schritt soll der eigentliche Baum anhand der Frequenz-Blätter aufgebaut werden:

def build_tree(freqs):
    def sortkey(node):
        return (node[1], node[0])
    nodes = sorted(freqs, key=sortkey)
    while (len(nodes) > 1):
        a = nodes[0]
        b = nodes[1]
        c = Node(sorted(a.chars + b.chars), a.weight + b.weight, a, b)
        nodes = sorted([c] + nodes[2:], key=sortkey)
    return nodes[0]

Die Hilfsfunktion sortkey sortiert die Knoten aufsteigend nach Häufigkeit und Zeichen(folge). Solange es mehr als einen Knoten in der Liste gibt, werden die Knoten mit den jeweils geringsten Frequenzen paarweise kombiniert. Dabei werden die Zeichen als Strings zusammengehängt, und die Gewichte (Häufigkeiten) aufaddiert. Die Liste mit den Knoten wird neu erstellt, sodass die beiden Kinder daraus verschwinden und nur noch ihr gemeinsamer Eltern-Knoten darin auftaucht. Sobald die Liste nur noch aus dem Wurzelknoten besteht, ist der Baum fertig aufgebaut.

Kodierung

Für die eigentliche Kodierung soll ein spezieller Datentyp namens BitStream aus dem entsprechenden Package (bitsream) zum Einsatz kommen:

from bitstream import BitStream

def encode(text, tree):
    bits = BitStream()
    for c in text:
        bits.write(encode_char(c, tree))
    return bits

Jedes Zeichen im Text soll anhand des Baumes und der Hilfsfunktion encode_char kodiert werden. Diese ist folgendermassen implementiert:

def encode_char(c, tree):
    path = []
    if len(tree.chars) == 1 and c == tree.chars[0]:
        # leaf
        return path
    elif c in tree.chars:
        # node
        if c in tree.left.chars:
            return path + [left] + encode_char(c, tree.left)
        elif c in tree.right.chars:
            return path + [right] + encode_char(c, tree.right)
        else:
            raise ValueError(f'{c} not found in left/right branch of {tree}')
    else:
        raise ValueError(f'{c} not found in {tree}')

Der Baum wird von oben nach unten durchlaufen. Der dabei beschrittene Pfad wird in der Liste path als Bitfolge festgehalten. Handelt es sich beim aktuell besuchten Knoten um ein Blatt (ein Zeichen, das dem zu kodierenden entspricht), ist die Bitfolge komplett. Bei Knoten mit mehreren Zeichen und Kindern muss der richtige Pfad eingeschlagen werden, indem das zu kodierende Zeichen in den beiden Kindern links und rechts gesucht wird.

Die eigentliche Kodierung kann nun anhand der bereitgestellten API erfolgen:

if __name__ == '__main__':
    text = 'abracadabra'
    freqs = count_frequencies(text)
    tree = build_tree(freqs)
    encoded = encode(text, tree)
    print(f'Compressed "{text}" as {encoded} in {len(encoded)} bits.')

Und so wird es ausgeführt:

$ ./huffman.py
Compressed "abracadabra" as 01101001110011110110100 in 23 bits.
…

12 Zeichen in 23 (Huffman) statt 96 (ASCII) Bits: nicht schlecht!

Dekodierung

Das bringt aber nur etwas, wenn man das wieder rückgängig machen kann. Hierzu wird eine Funktion zur Dekodierung benötigt:

def decode(bits, tree):
    text = ''
    bits = bits.copy()
    while len(bits):
        char, bits = decode_next(bits, tree)
        text += char
    return text

Begonnen wird mit einem leeren Text; die Bitfolge wird kopiert, damit das Original erhalten bleibt. Das jeweils nächste Zeichen wird mit decode_next dekodiert, wonach eine kürzere Bitfolge verbleibt:

def decode_next(bits, tree):
    if len(tree.chars) == 1:
        # leaf
        return tree.chars[0], bits
    elif len(bits):
        # node
        bit = bits.read(bool, 1)[0]
        if bit is left:
            return decode_next(bits, tree.left)
        else:
            return decode_next(bits, tree.right)
    else:
        raise ValueError('bits consumed prematurely')

Verfügt der jeweilige (Unter)baum (tree) nur noch über ein einziges Zeichen, ist ein Blatt erreicht, und das Zeichen kann mit der verbleibenden Bitfolge zurückgegeben werden. Sind jedoch mehrere Zeichen im Ast zu finden und noch Bits vorhanden, wird der Bitfolge das nächste Bit entnommen, welches uns in die linke oder rechte Richtung herabschickt, wozu decode_next rekursiv aufgerufen wird.

Die vorher erstellte (kodierte) Bitfolge wird folgendermassen dekodiert:

if __name__ == '__main__':
    # …
    encoded = encode(text, tree)
    # …
    decoded = decode(encoded, tree)
    print(f'Decompressed {encoded} as "{text}".')

Auch das funktioniert:

$ ./huffman.py
…
Decompressed 01101001110011110110100 as "abracadabra".

Und jetzt?

Jetzt müsste nur noch ein Dateiformat gefunden werden, in die sich die Bitfolge zusammen mit dem Kodierungsbaum effizient abspeichern liesse. Doch dieses Problem ist durch gzip, bzip2, xz usw. schon gelöst. Hier soll es ja nur um das Verständnis gehen.

Das ganze, ausführbare Programm steht als GitHub Gist zur Verfügung. Eine alternative Implementierung in Erlang kann die kodierte Bitfolge inkl. Huffman-Baum in einer Datei ablegen und auch wieder daraus herauslesen und dekodieren.